近日，《力学学报》刊登了武汉大学周伟教授团队的最新研究成果。该研究分析了颗粒试验在剪切过程中自由体积的统计分布特性和演化规律，研究了颗粒形态对自由体积的影响。研究论文题为“椭球颗粒体系剪切过程中自由体积的分布与演化”，马刚副教授为通讯作者。

1 研究背景

虽然颗粒材料的结构特性与其物理力学性质的相关性已经得到大量研究证明，但是具有复杂颗粒形状和宽粒径分布的颗粒材料的结构表征，以及建立宏观力学响应和细观结构的联系仍是一个重大挑战。

2 模型和方法

采用连续离散耦合分析方法模拟了7种主轴长度不同的椭球颗粒试样的三轴剪切试验，试样图1所示。采用Domokos系数作为椭球颗粒的形状量化指标，定义为

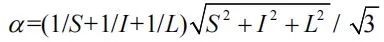
其中L、I、S分别代表椭球长轴、中轴和短轴的长度。

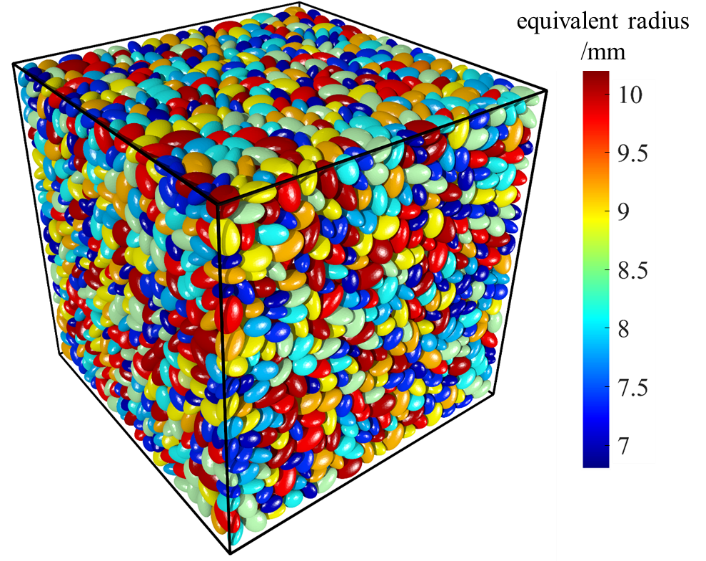
图1 数值试样

采用Set Voronoi剖分方法对椭球试样进行Voronoi元胞分割。具体步骤如图2所示：（1）在颗粒表面均匀分布足够多的点，得到每个颗粒表面的离散点集（2）计算所有颗粒表面离散点的Voronoi元胞（3）将属于同一颗粒的Voronoi元胞合并，形成该颗粒的Voronoi元胞。

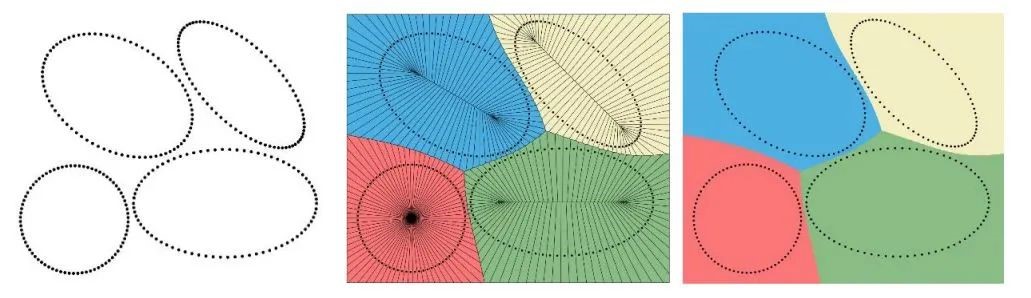
图2 Set Voronoi 剖分二维示意图

3 局部自由体积分布及演化规律

为了量化颗粒尺度自由体积的大小，引入局部孔隙比e_loc。

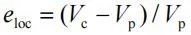
其中Vp和Vc分别为颗粒体积和其对应的Voronoi元胞体积。图3展示了不同非球度的椭球颗粒试样在剪切过程中局部孔隙比e_loc的概率密度分布。局部孔隙比e_loc服从k-gamma分布，在加载过程中e_loc分布逐渐向右移动，峰值减小并且分布范围更宽，这意味着颗粒在剪切过程中局部自由体积变大且分布更广。在加载后期这种演变逐渐趋于稳定，与试样先剪胀后达到临界状态的现象相吻合。

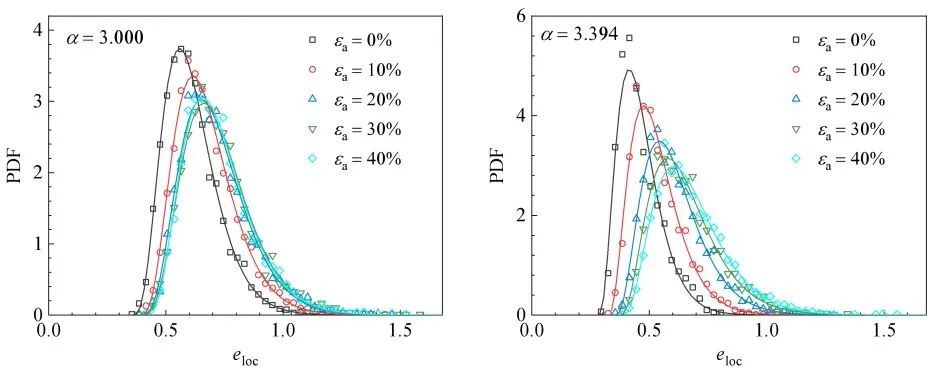
图3 不同非球度的椭球颗粒在不同加载阶段的局部孔隙比概率密度分布

图4为全局孔隙比e_glo时不同非球度的椭球颗粒试样的局部孔隙比的概率密度分布，此时七组试样剪切状态不同，轴向应变分别为9.0%、12.7%、15.2%、21.0%、27.1%、31.8%和37.7%。可以发现不同非球度试样的局部孔隙比分布基本一致，这说明颗粒局部孔隙比的分布仅与全局孔隙比相关，不受颗粒形态和剪切状态的影响。

图4 不同非球度的椭球颗粒在全局孔隙比相同时局部孔隙比概率密度分布

从局部孔隙比分布的演化可知剪切过程中局部自由体积的变化是非均匀的。选取了5个加载阶段（ε_a=4%、10%、20%、30%和40%），分析不同非球度的椭球颗粒试样在应变窗口Δε_a≈0.8%的局部孔隙比波动。图5为不同非球度的椭球颗粒试样在不同加载阶段的局部孔隙比波动的概率密度分布。局部孔隙比的波动呈现非对称拉普拉斯分布（Asymmetric Laplace Distribution, ALD），其函数为：

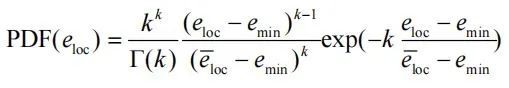
Δe_loc的分布可以分为左右两个非对称的指数函数（在单对数坐标系下表现为斜率不一致的两段线性分布），分界点在Δe_loc=0附近。左右两侧分布的非对称性刻画了局部自由体积收缩和膨胀的博弈。随着剪切进行，代表体积膨胀的右侧体积波动分布变化较小，而左侧分布的斜率有明显下降，两侧趋于对称，即剪胀会随剪切过程逐渐停止。

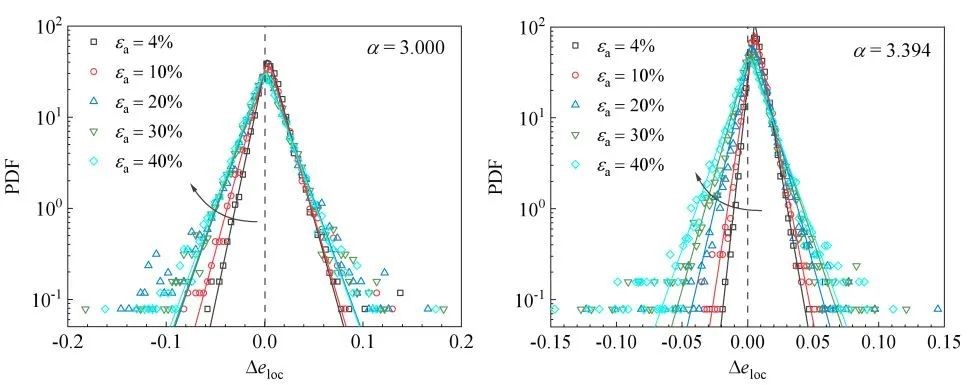
图5 不同非球度的椭球颗粒试样在不同加载阶段的局部孔隙比波动概率密度分布

ALD中非对称参数k为分布两侧斜率比值的平方，描述了ALD的非对称程度，也刻画了体积膨胀的强度。k越小体积膨胀越明显，k=1时体积无变化。如图6所示，k与全局孔隙比e_glo呈现明显的线性关系，并在k=1附近截断。这意味着体积膨胀的强度很大程度上取决于试样当前全局孔隙与临界全局孔隙比的差值，故随α增大体胀更显著可以归因于椭球颗粒在相同固结条件下可以形成更密实的堆积。

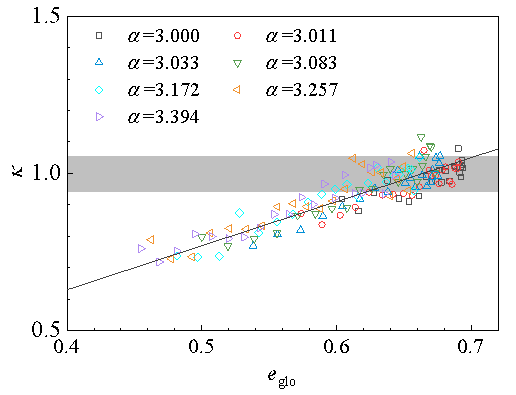
图6 非对称参数与全局孔隙比的关系

4 结论

不同椭球颗粒试样的局部孔隙比均服从k-gamma分布，且这个分布仅与全局孔隙比相关，不受颗粒形态和剪切状态的影响。非球度更大的颗粒在剪切过程中会产生更强烈的重排列，导致局部孔隙比和Voronoi元胞球度在剪切过程中的变化随颗粒形状参数α的增大而增大。

不同非球度的椭球颗粒试样的局部孔隙比波动均服从非对称拉普拉斯分布，这种不对称性刻画了局部自由体积收缩和膨胀的博弈。非对称参数与全局孔隙比呈现明显的线性关系，表明体积膨胀的强度很大程度上取决于试样当前全局孔隙此与临界全局孔隙比的差值。

通讯作者：马刚

联络邮箱：magang630@whu.edu.cn  (马刚)

研究方向：

连续离散耦合数值分析方法
岩土颗粒材料的宏细观多尺度力学特性

论文链接：https://lxxb.cstam.org.cn/cn/article/doi/10.6052/0459-1879-21-255